| - PR - |
| <No6:基準点測量:解答> 多角測量における方向角の計算問題である。次図のように図中に補助線を加えて順序良く計算すれば解くことができる。公式を覚えるよりは、次図のような図を描き解けるようにした方が良い。 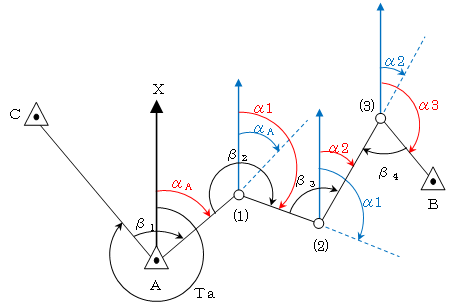 図より、新点(3)における既知点Bへの方向角(α3)を求めるには、αAから順番に方向角を求めればよい。 ・A点における(1)への方向角 αA=(TA+β1)-360°= (320°16′40″+ 92°18′22″)- 360°= 52°35′02″ ・(1)点における(2)への方向角 α1=(αA+β2)-180°= (52°35′02″+ 246°35′44″)- 180°= 119°10′46″ ・(2)点における(3)への方向角 α2=(α1+β3)-180°= (119°10′46″+ 99°42′04″)- 180°= 38°52′50″ ・(3)点におけるBへの方向角 α3+β4-180°=α2 であるため、 α2=α3-β4+180°= 38°52′50″- 73°22′18″+ 180°= 145°30′32″ ※各方向角とも、図を参照して式を導きだすのが基本である。 よって、新点(3)における、既知点Bの方向角は、145°30′32″となる。 |
| 解答:4 |